What if we programmed a computer to sleep, perchance to dream? As it turns out, some researchers have already tried. During spring break, I read a fascinating paper titled DreamCoder: Growing generalizable, interpretable knowledge with wake-sleep Bayesian program learning by Ellis et. al. from MIT CSAIL.
As humans, we can learn rules, patterns, and hallmark features from just a few examples. We only need a few pictures to place a new face, a few repetitions of the same grammatical structure to extrapolate a rule. Imagine being asked to pick up a stranger from the airport with only a handful of photos—we could do it. Our innate ability to generalize has become some what of a holy grail for artificial intelligence researchers, who call this skill few-shot learning.
Achieving few-shot learning is one of the main motivations of the DreamCoder paper. The authors wondered if machines, like humans, could be learn how to generalize and learn from just a few examples. While the state of the art trends toward deep and data-hungry networks, the authors decided that instead of approaching the problem neurally, with an avalanche of data fed to a neural network, they would approach it symbolically, by teaching a computer how to create building blocks for a variety of problems. The premise of DreamCoder was to see if machines could learn symbolic program synthesis, or how to write a program for any problem.
The key word is any. One of the highlights of DreamCoder was the generalizability and performance it demonstrated as it was applied to numerical processing, pattern learning, image generation, programming tasks, and theoretical work. Loftily, the authors wrote "it [DreamCoder] rediscovers the basics of modern functional programming, vector algebra and classical physics, including Newton's and Coulomb's laws."

DreamCoder solves problems by writing programs—coding, if you will. These programs are reminiscent of Lisp, lambda calculus expressions involving a vocabulary of 'cons', 'cdr', and 'cars', but which otherwise come with the standard vocabulary of conditionals, variables, and function composition. In a process that amounts to search and with the guidance of a helper neural network providing domain-specific knowledge, DreamCoder learns to write programs to sort lists, draw towers, and theorize like a lite Isaac Newton.
“DreamCoder learns explicit declarative knowledge, in the form of a learned domain-specific language, capturing conceptual abstractions common across tasks in a domain; and (2) implicit procedural knowledge, in the form of a neural network that guides how to use the learned language to solve new tasks, embodied by a learned domain-specific search strategy.
In Bayesian terms, the system learns both a prior on programs, and an inference algorithm (parameterized by a neural network) to efficiently approximate the posterior on programs conditioned on observed task data.” [From the paper]
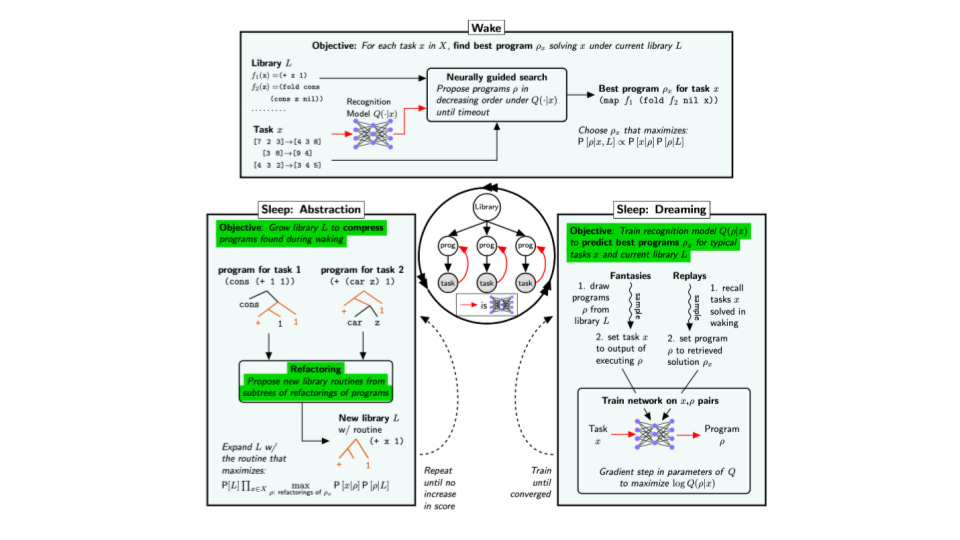
But how did DreamCoder achieve this jack-of-all-trades dexterity? The answer is by using wake-sleep learning, the technique and namesake of the paper, to write programs. This bio-inspired approach borrows high-level concepts for our REM sleep cycles. Just as we learn during the day and dream during the night in phases that consolidate our memories, DreamCoder also learns in a bifurcated process. During its wake phase, the generative model interprets new data. During its sleep phase, it imagines new problems to solve, "dreaming".
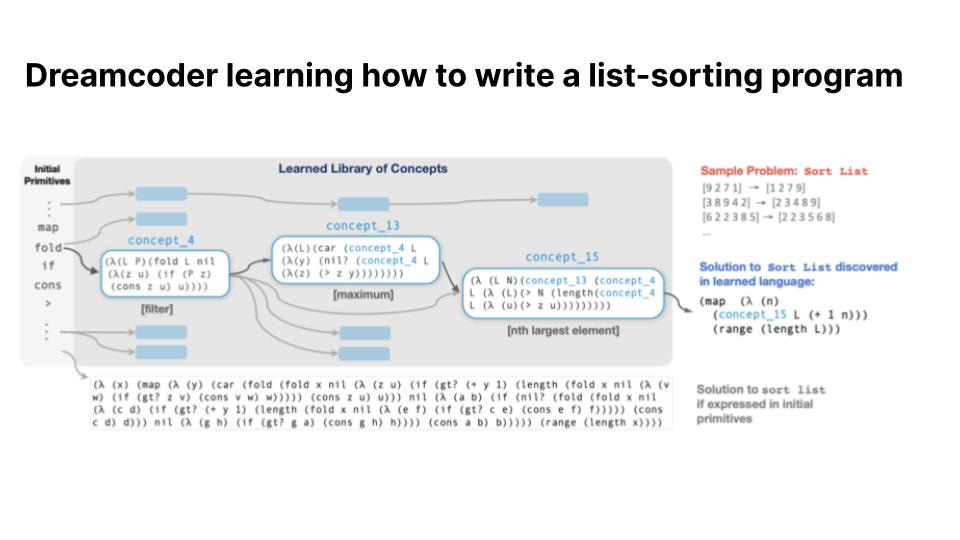
For example, let's step through how DreamCoder might learn how to write a list-sorting program. First, it would be given a number of examples of random numbers and their proper sequencing in ascending order. DreamCoder’s objective is to find a solution that can sort numbers in this ascending order, to write a learned language such as the following:
(map (lambda (n) concept_15 ...))To do so, DreamCoder starts off with a base library of primitives: map, fold, if, and cons. Throughout the learning stage, these primitives recursively build into more complex concepts. Early on, concepts for filtering, maximum, and finding the nth largest element (selection) are learned. By inference time, more complicated concepts can be utilized to write what the authors argue as human legible programs.
The phase that I find more interesting is sleep, which takes place under two processes: abstraction and dreaming. As the program learns, the library grows in length. During the stage of abstraction, common code fragments of the solutions DreamCoder came up with are replayed and abstracted into new primitives. This is how from simple primitives, more complicated concepts are formed. This abstraction is implemented through a crude optimization on the length of the library and the length of written programs. Alternating with this consolidation is DreamCoder's computational approach to dreaming. Dreaming is a process that trains the neural network which guides the search during "wake" time using "fantasies".
Visuals help make this narrative concrete. Take for example DreamCoder applied to a drawing task.
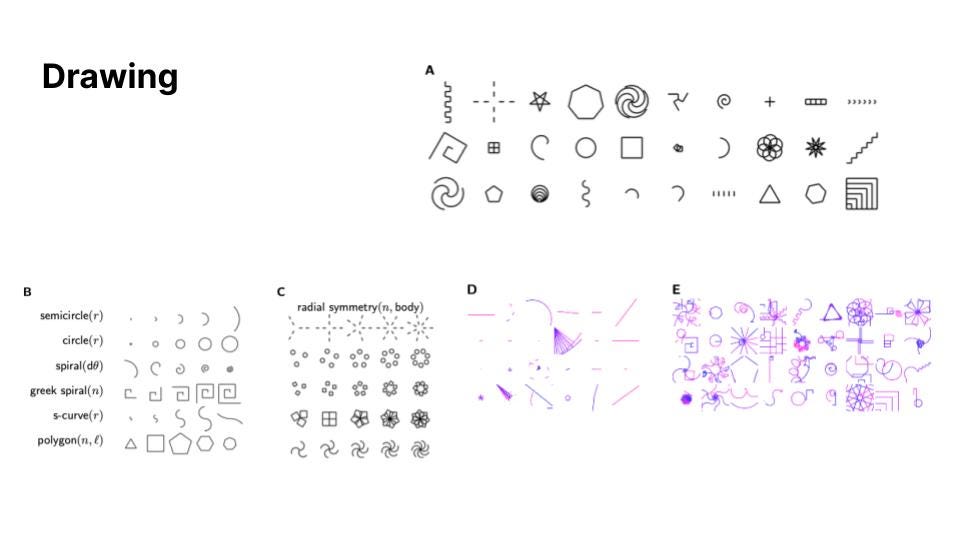
After showing DreamCoder examples of spirals, fractals, and zigzags, DreamCoder is able to surmise a number of high level geometric and visual concepts: semicircles, spirals, greek spirals, s-curves, polygons, and so forth. From these, it is able to go a level further and write higher level programs. If we zoom into the parts of the figure above, we can see an evolution in the dreaming process. At first, we can see random, simple chaos in the dreams (part D). However, as the training progresses with the neural network, we can see that the dreams become more rich in complexity in expressive in variety (part E). Furthermore, in later stages of learning, DreamCoder exhibited the capacity to write higher-order functions. The functions in part C demonstrated how a function could apply radial symmetry on polygons of choice, which were functions in themselves.
These observations as the authors considered a different but also visual domain—tower building.
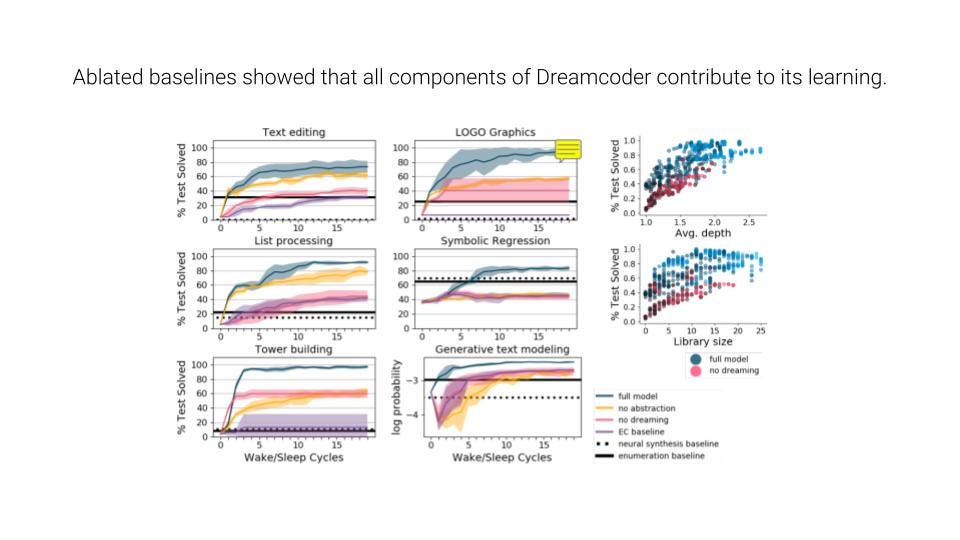
Research is just as much about the evaluation as it is about the system, and DreamCoder's evaluations found that all components of DreamCoder contributed to how it learned. They found this using ablated baselines, where some phases of DreamCoder were toggled off. (For example, they looked at DreamCoder the full model, DreamCoder minus abstraction, DreamCoder minus dreaming, and so on.)
Throughout the paper, the breadth of what DreamCoder's symbolic approach to learning was hammered home through the number of domains the researchers pivoted DreamCoder towards. Beyond the stereotypical computation and visual tasks, DreamCoder had the capacity to solve more symbolic problems. It had the capacity to "rediscover" origami folding, one of the fundamental elements of recursive programming, and it had the capacity to “rediscover” physics by formulating functions for the laws of kinetic energy and parallel resistors.
Nonetheless, DreamCoder was not without caveats. Approaches like DreamCoder are constrained by toy problems and problems that are well parameterized. For example, generating and manipulating image data like faces or animal photos as vanilla convolutional networks well tuned to doing is out of scope for DreamCoder.
My main takeaways from this paper are that DreamCoder shows the promise of neurosymbolic systems, a class of systems that combine symbolic and neural learning approaches. State of the art deep models are ingrained with a tunnel vision, as they are beholden to whatever narrow class of data they are trained upon. However, DreamCoder provides a model that is arguably loosely in line with how we learn: through few examples, solution synthesis, and an everlasting cycle of waking, sleeping, and dreaming.
References
Kevin Ellis, Catherine Wong, Maxwell Nye, Mathias Sable-Meyer, Luc Cary, Lucas Morales, Luke Hewitt, Armando Solar-Lezama, Joshua B. Tenenbaum. DreamCoder: Growing generalizable, interpretable knowledge with wake-sleep Bayesian program learning. https://arxiv.org/abs/2006.08381